Come costruire la curva di trasformazione
Per disegnare la curva di trasformazione di due beni occorre conoscere le funzioni di produzione dei beni in questione.
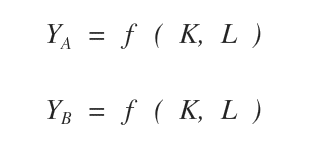
Una volta conosciute le quantità producibili Y dei beni A e B, bisogna individuare quali combinazioni ( YA, YB ) sono ottimi di produzione.
Cos'è un ottimo di produzione? Secondo la definizione di Pareto, si parla di ottimo di produzione quando non è possibile aumentare la produzione di un bene senza ridurre quella dell'altro bene.
Come cercare gli ottimi di produzione
Parto da un esempio pratico. Ho un terreno e devo decidere quanto grano (A) e quante patate (B) coltivare.
Entrambe le produzioni usano gli stessi fattori produttivi: il lavoro ( L ) e il capitale ( K ).
Per ogni bene A e B calcolo gli isoquanti in base alle rispettive condizioni tecnologiche di produzione.
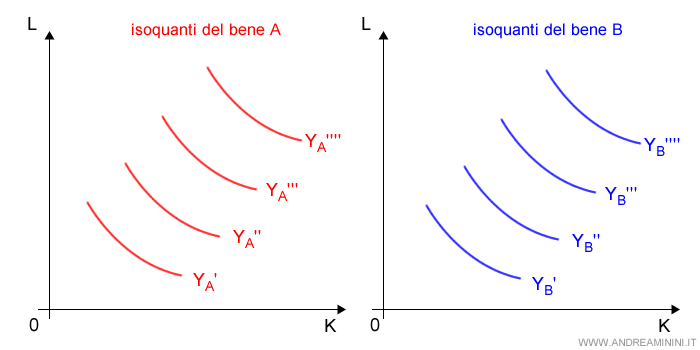
Cosa sono gli isoquanti? La curva di un isoquanto indica le combinazioni dei fattori produttivi ( K , L ) che consentono di produrre la stessa quantità finale di un bene ( Y ). Gli isoquanti più esterni indicano una maggiore quantità di produzione. Pertanto, YA' < YA".
A questo punto ruoto di 180° il secondo diagramma.
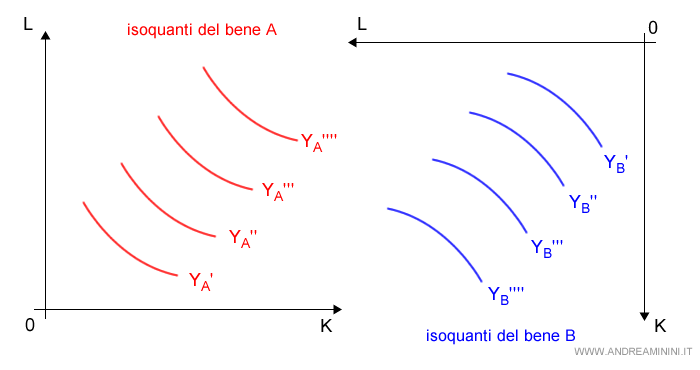
Poi sovrappongo il secondo diagramma sul primo.
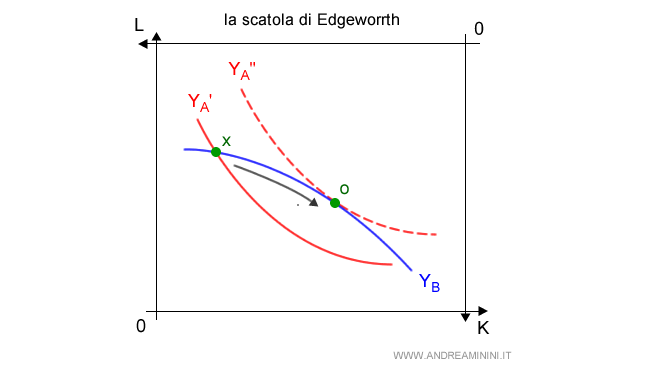
Questo diagramma sovrapposto è conosciuto come Scatola di Edgeworth.
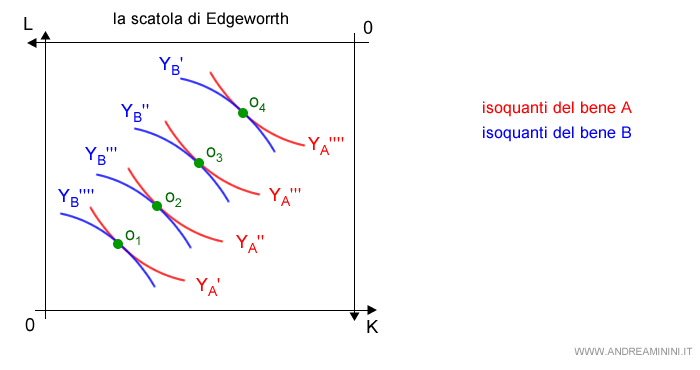
In alcuni punti della Scatola di Edgeworth gli isoquanti di un bene (grano) sono tangenti all'isoquanto dell'altro bene (patate).
Questi punti di tangenza degli isoquanti ( o1, o2, o3, o4 ) sono gli ottimi di produzione.
Ho così calcolato le quantità ottimali di produzione di entrambi i beni.
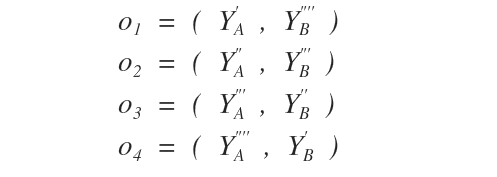
Nota. Nei punti di tangenza degli isoquanti i fattori produttivi K e L hanno lo stesso saggio marginale di sostituzione, perché la retta tangente ha la stessa inclinazione. In questa circostanza non posso incrementare la produzione di un bene senza ridurre la produzione dell'altro bene ( ottimo paretiano ). Viceversa, se mi trovassi in un altro punto dove i saggi marginali di sostituzione sono diversi ( es. punto X ), potrei modificare la combinazione dei fattori ( K, L ) per aumentare la produzione del bene A ( passando dall'isoquanto rosso Y'A a Y"A ) senza ridurre la produzione di YB ( stesso isoquanto blu ).
A questo punto, disegno un altro diagramma con le quantità di produzione del primo bene sulle ascisse e del secondo bene sulle ordinate.
Poi disegno gli ottimi di produzione nelle relative coordinate ( YA, YB ).
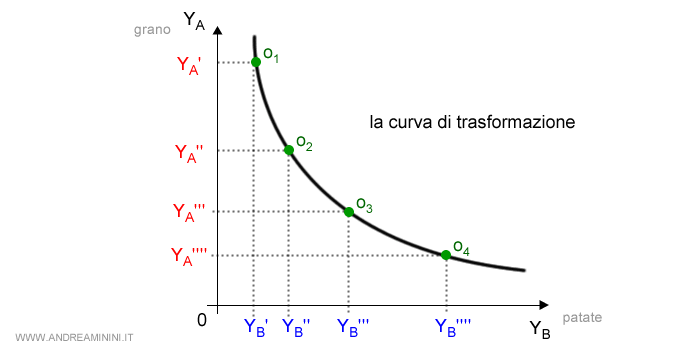
Congiungendo gli ottimi di produzione ottengo la curva di trasformazione dei beni A e B.
In questo modo ho costruito la curva di trasformazione dei beni a partire dalla loro funzione di produzione.
