La curva di indifferenza

Cos'è una curva di indifferenza

Una curva di indifferenza collega tutti i panieri di consumo che forniscono la stessa utilità complessiva al consumatore.

Ogni punto sulla curva rappresenta un paniere composto da due beni $x$ e $y$. Se due panieri si trovano sulla stessa curva, significa che per il consumatore sono equivalenti: non preferisce né l’uno né l’altro.

Esempio. Se un consumatore considera ugualmente soddisfacenti i panieri A = (5 mele, 15 pere) e B = (15 mele, 5 pere), allora A e B giacciono sulla stessa curva di indifferenza, poiché gli forniscono la stessa utilità.

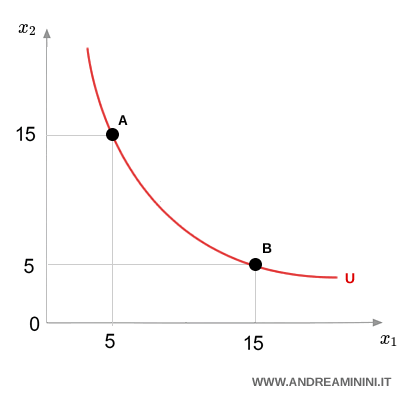
A cosa serve?

E' uno strumento grafico che rappresenta le preferenze di un consumatore tra diversi panieri di beni.

Serve a capire quali combinazioni di due beni generano lo stesso livello di soddisfazione, cioè di utilità, per il consumatore.

Nota. La curva di indifferenza aiuta a visualizzare le scelte del consumatore e a capire come valuta i compromessi tra beni. È uno strumento base per studiare l’ottimo del consumatore, quando si combina con il vincolo di bilancio.

Utilità e confronto tra panieri

Ogni curva rappresenta un livello di utilità costante, quindi più curve rappresentano diversi livelli di utilità.

Le curve più lontane dall’origine indicano maggiore utilità.

Questo riflette quello che viene chiamato l’assioma di non sazietà, ossia a parità di tutto il resto, il consumo di più beni genera più soddisfazione.

Esempio

Un consumatore deve scegliere tra due beni $ x_1 $ e $ x_2 $

Ha a disposizione tre panieri:

$$ A = (5,10) $$

$$ B = (10,10) $$

$$ C = (15,10) $$

Il paniere C è su una curva più alta di B, che a sua volta è su una curva più alta di A.

Quindi, secondo l'assioma di non sazietà, il consumatore preferisce C a B, e B ad A.

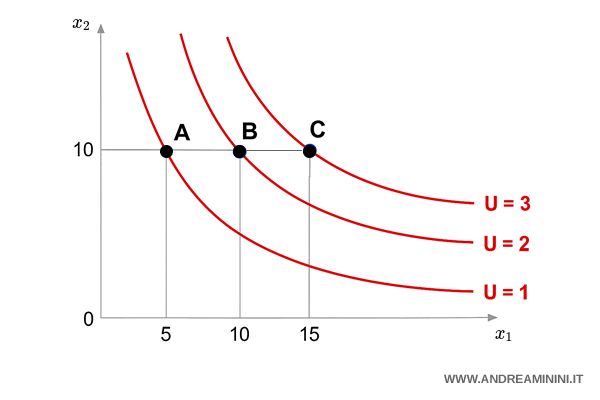
Del resto con il paniere C ottiene 15 unità del bene $ x_1 $ e 10 unità del bene $ x_2 $.

Negli altri due panieri A e B c'è una minore quantità di beni.

Le proprietà delle curve di indifferenza

Le curve di indifferenza hanno alcune caratteristiche fondamentali:

• Inclinazione negativa: se aumenta la quantità di un bene, quella dell’altro deve diminuire per mantenere costante l’utilità.
• Convessità verso l’origine: il consumatore preferisce combinazioni bilanciate di beni. Questo è dovuto all’utilità marginale decrescente: ogni unità aggiuntiva di un bene vale meno se se ne possiede già tanto.
• Non si intersecano mai: ogni curva corrisponde a un livello unico di utilità. L'intersezione violerebbe la coerenza delle preferenze.

L'inclinazione della curva di indifferenza

La curva di indifferenza è decrescente perché all’aumentare del consumo di un bene, bisogna diminuire l’altro per restare sullo stesso livello di utilità.

Questo deriva dalla scarsità: le risorse del consumatore sono limitate, e per ottenere di più da un lato, deve sacrificare qualcosa dall’altro.

Per questa ragione la curva ha un'inclinazione negativa.

Esempio. Se un individuo ha solo 10 euro da spendere tra pane e formaggio, più pane acquista, meno formaggio potrà permettersi.

Quindi, l’inclinazione della curva di indifferenza non è solo una nozione geometrica: è il riflesso grafico di come ragiona un consumatore razionale in condizioni di scarsità delle risorse.

Dal punto di vista tecnico l’inclinazione misura il Saggio Marginale di Sostituzione (SMS) tra due beni, ad esempio $X_1$ e $X_2$.

Questo valore esprime quanta quantità del bene $X_2$ il consumatore è disposto a cedere per ottenere un’unità aggiuntiva di $X_1$, senza variare il proprio livello di utilità. 

Convessità della curva

Le curve di indifferenza sono convesse verso l’origine perché i consumatori hanno la tendenza razionale a preferire panieri bilanciati, piuttosto che estremi.

• Nei tratti dove un bene è abbondante, la curva si appiattisce.  Questo significa che l’utilità marginale di quel bene è bassa, in quanto il consumatore ha già consumato una notevole quantità di quel bene.
• Nei tratti dove un bene è scarso la curva è più inclinata. In questi tratti l’utilità marginale è alta, perché il consumatore ne ha consumato poché unità rispetto all'altro.

Esempio

Un consumatore può acquistare 20 unità del bene $ x_1 $ (ad esempio, pere) oppure 20 unità del bene $ x_2 $ (ad esempio, mele).

Può anche optare per panieri misti. Il paniere A = (15, 5), ad esempio, contiene 15 unità di pere e 5 di mele. 

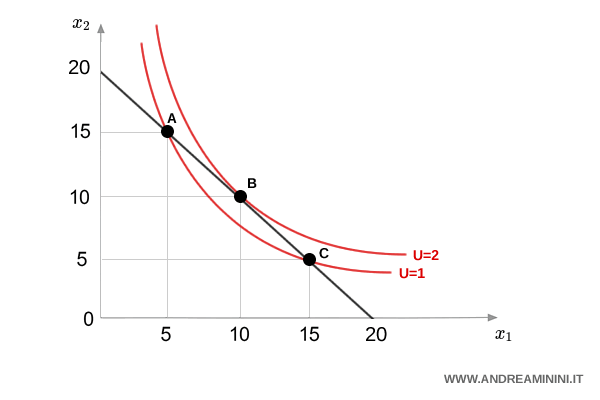
A parità di spese, un consumatore razionale preferirà il paniere intermedio B = (10, 10) che si trova su una curva di indifferenza più esterna (U=2), e quindi è associato a un livello di utilità maggiore.

In altre parole un paniere come B(10,10) è preferibile rispetto a A(15,5) o C(5,15), poiché rappresenta una combinazione più equilibrata dei due beni e fornisce un'utilità maggiore, rispecchiando la preferenza per varietà del consumatore.

Questo spiega la forma convessa della curva di indifferenza.

Nota. L'assioma di non sazietà, ossia “più è meglio”, è una semplificazione usata per spiegare la teoria delle preferenze individuali, considerando i consumatori come persone che agiscono razionalmente e con tutte le informazioni a loro disposizione. Il cosiddetto "homo economicus". La realtà non è esattamente così... ma per il momento facciamo finta che lo sia.

Il saggio marginale di sostituzione (SMS)

Il Saggio Marginale di Sostituzione (SMS) indica quante unità di un bene il consumatore è disposto a cedere per ottenere un’unità in più dell’altro bene, senza cambiare il livello di utilità.

Quindi, si tratta di uno spostamento sulla stessa curva di indifferenza, perché il livello di utilità resta costante.

In termini di variazione del consumo dei beni, la formula del saggio marginale di sostituzione può essere scritta in questo modo:

$$ SMS = -\frac{Δx_1}{Δx_2} $$

Dove $ Δx_1 $ rappresenta la variazione di unità consumate del bene 1 e $ Δx_2 $ quella del bene 2.

Ad esempio, se il consumatore è disposto a scambiare 1 arancia ( bene $ x_2 $ ) per 2 mele ( bene $ x_1 $ ), allora il SMS è 2. In altre parole, il consumatore è disposto a cedere 1 unità del bene $ x_2 $ (arance) per ottenere 2 unità in più del bene $ x_1 $ (mele). Questo significa che una mela ha metà del valore marginale di un’arancia in quel punto della curva di indifferenza. $$ SMS =  -\frac{Δx_1}{Δx_2} = - \frac{2}{-1} =2 $$

In termini di utilità marginali, lo stesso rapporto si esprime con questa formula:

$$ \frac{Δx_1}{Δx_2} = - \frac{UM_{x_2}}{UM_{x_1}} $$

Dove $ UM_{x_1} $ è l'utilità marginale del bene 1 mentre $ UM_{x_2} $ è quella del bene 2.

Del resto lo spostamento avviene mantenendo costante l'utilità, quindi l'incremento di utilità ottenuto dal maggiore consumo di un bene deve essere compensato dalla perdita di utilità dovuta al minore consumo dell'altro bene.

$$ Δx_1 \cdot UM_{x_1} = - Δx_2 \cdot UM_{x_2} $$

Dal punto di vista grafico il SMS indica la pendenza della curva di indifferenza in un punto, ovvero la pendenza della retta tangente nel punto in questione.

Per questa ragione, spesso conviene indicarlo usando variazioni infinitesimali del consumo dei beni.

$$ SMS = -\frac{dx_1}{dx_2} $$

E così via.