Decision Theory

What is Decision Theory, and how can it transform the way we choose?

Every day, we’re faced with choices - investing money, switching careers, even picking what to eat for lunch. But have you ever paused to think about how you actually make those decisions? Decision theory dives into this process, using mathematical and statistical models to help us make better choices - especially when uncertainty enters the picture.

How Decision Theory Works

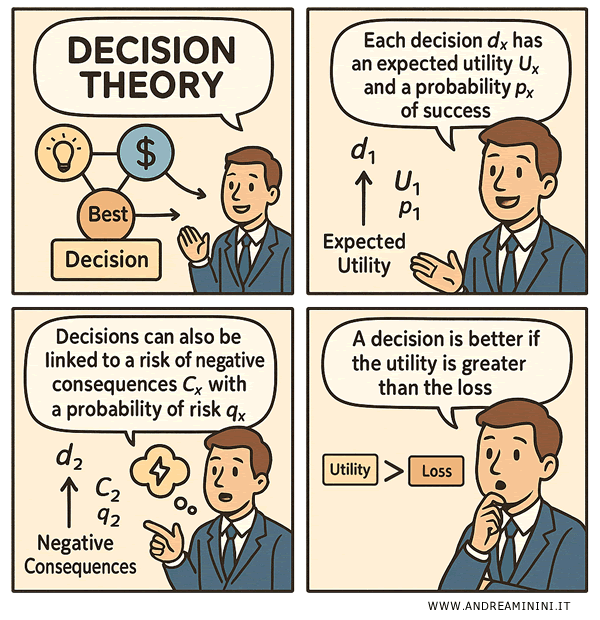
At its core, decision theory is built on one simple but powerful principle: when facing several options, a rational person chooses the one that maximizes expected utility. In plain terms, you go with the option that promises the greatest benefit - or the least regret.

Every decision \( d_x \) has two key elements:

• Utility \( U_x \): the potential value or payoff you stand to gain.
• Probability of success \( p_x \): how likely it is that things will go as planned.

But no decision is risk-free. Every choice can also involve:

• Negative consequences \( C_x \): possible costs, damages, or losses.
• Risk probability \( q_x \): the chance that things might go wrong.

The golden rule? A smart decision is one where the expected benefit outweighs the possible risks.

Who Laid the Foundations of Decision Theory?

Decision theory didn’t appear out of thin air. It was shaped by brilliant minds like Abraham Wald, who introduced the idea of "optimal decision-making" under uncertainty, and John von Neumann, a pioneer in game theory who bridged mathematics, economics, and human behavior. Their groundbreaking work in the early 20th century continues to guide millions of decisions today - in business, government, healthcare, and beyond.

For example, in economics, decision theory explains how investors and consumers weigh their options. In engineering, it helps plan safer, smarter projects. In medicine, it supports doctors in choosing the best treatment paths for patients, and so much more.

Real-World Examples

Let’s break it down with a few practical examples.

Example 1

I’m deciding where to invest my savings. Suppose I have two choices:

• Investment A: earn up to €8,000, with a 70% chance of success.
• Investment B: earn up to €12,000, but with only a 40% chance of success.

To make a rational choice, I calculate the expected utility:

• Expected Utility A = €8,000  × 0.7 = €5,600
• Expected Utility B = €12,000 × 0.4 = €4,800

Which one’s smarter? In this case, Investment A - because it offers the higher expected payoff.

Example 2

Now, let’s say I’m thinking about launching a new product. Here’s the situation:

• Potential profit: €40,000
• Chance of success: 65%
• Possible loss if it fails: €15,000
• Chance of failure: 35%

Here’s the net expected value:

$$ (40,000 \times 0.65) - (15,000 \times 0.35) = 26,000 - 5,250 = 20,750€ $$

Should I launch? Based on the numbers, yes - the expected return is clearly positive.

Note. Of course, real-life decisions aren’t always this clean. Your personal risk tolerance matters a lot, and estimating probabilities isn’t always easy. That’s why "risk" and "uncertainty" are two different beasts - each with its own challenges.

Risk vs. Uncertainty: What’s the Difference?

Decision theory draws a clear line between two types of situations:

• Risk: you know the odds (think betting, insurance policies).
• Uncertainty: the odds are unknown or fuzzy (think launching a brand-new startup).

When you’re under risk, you can crunch the numbers and make rational calls. When you’re under uncertainty, you often have to lean on experience, gut feeling, or more cautious strategies.

Example. A farmer, knowing the summer weather will be unpredictable, chooses a hardy but less profitable crop. Why? To lower the chance of total loss.

Bottom line: Decision theory won’t make you immune to mistakes, but it gives you a solid framework to make smarter, more thoughtful choices - steering you away from leaving everything to luck or impulse.