Avversione al rischio

L’avversione al rischio è una caratteristica psicologica che descrive la tendenza di un individuo a preferire situazioni certe rispetto a situazioni incerte, anche quando queste ultime offrono lo stesso valore economico atteso.

In altri termini, una persona avversa al rischio preferisce un guadagno sicuro inferiore a una scommessa che potrebbe dare di più, ma che comporta anche la possibilità di perdere.

Nota. L’avversione al rischio è uno dei principi fondamentali dell’economia comportamentale e della teoria delle decisioni. Spiega perché le persone sottoscrivono assicurazioni, evitano investimenti volatili e accettano compromessi pur di avere certezza.

Se considero una lotteria con due possibili esiti monetari, $X_1$ e $X_2$, che si verificano con probabilità rispettive $p_1$ e $p_2$, tali che $p_1 + p_2 = 1$, il valore atteso della lotteria è:

$$   E(X) = p_1 \cdot X_1 + p_2 \cdot X_2   $$

L’utilità attesa è:

$$ E(U) = p_1 \cdot U(X_1) + p_2 \cdot U(X_2)  $$

L’utilità del valore atteso è invece:

$$   U(E(X))   $$

Quindi, un individuo è avverso al rischio se l'utilità del valore atteso è maggiore dell'utilità attesa:

$$ U(E(X)) > E(U) $$

Questo significa che l'individuo preferisce ricevere il valore atteso della lotteria con certezza, piuttosto che parteciparvi.

Esempio pratico

Supponiamo una lotteria in cui c’è il 50% di probabilità di vincere 100€ e il 50% di probabilità di vincere 0€

In questo caso il valore atteso è:

$$ E(X) = 0.5 \cdot 100 + 0.5 \cdot 0 = 50€ $$

Se un individuo preferisce ricevere 45€ certi piuttosto che partecipare alla lotteria, significa che è disposto a rinunciare a 5€ pur di evitare il rischio.

Questo importo (5€) è detto premio per il rischio: la quantità che l’individuo è disposto a “pagare” per non essere esposto all’incertezza.

Rappresentazione grafica

Per rappresentare l'attitudine al rischio sul piano cartesiano, sull’asse orizzontale metto il valore monetario $x$ mentre sull'asse verticale l’utilità $U(x)$

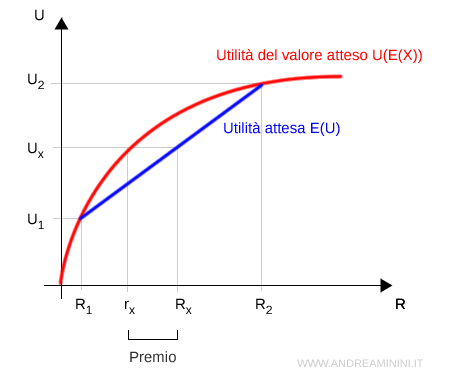
La linea rossa curva rappresenta la funzione di utilità del soggetto. È concava, a indicare un comportamento avverso al rischio: l’utilità marginale della ricchezza diminuisce con l’aumentare della ricchezza.

La linea blu retta, invece, rappresenta l'utilità attesa della lotteria, calcolata come media ponderata delle utilità degli esiti $R_1$ e $R_2$, con rispettive probabilità.

Dove $Rx$ è il valore atteso della lotteria:

$$ Rx = p \cdot R_1 + (1-p) \cdot R_2 $$

Il valore $rx$ è l’equivalente certo, cioè la somma certa che il soggetto considera equivalente alla lotteria in termini di utilità.

La distanza orizzontale tra $Rx$ e $rx$ è detta premio per il rischio, è quanto il soggetto è disposto a “pagare” pur di evitare la lotteria e ricevere con certezza una somma minore.

Ad esempio, se la lotteria ha valore atteso 100€, ma il soggetto preferisce riceverne 90€, il premio per il rischio è 10€.

La disuguaglianza tra:

$$ U(Rx) > p \cdot U(R_1) + (1-p) \cdot U(R_2) $$

è visibile nel fatto che il punto sulla curva rossa (in corrispondenza di $R_x$)  è sopra il punto medio sulla retta blu.

Nota. Nel grafico l'utilità del valore atteso si trova sopra il segmento che unisce $U(X_1)$ e $U(X_2)$. Questo vuole dire che l'individuo può ottenere la stessa utilità $ U_x $ riducendo il valore monetario da $ R_x $ e $ r_x $, quindi è disposto a pagare un "premio" per ridurre il rischio. La distanza tra $E(X)$ e il valore $x$ che fornisce $E(U)$ rappresenta il costo psicologico del rischio  Se la funzione fosse lineare (e non concava), i due punti coinciderebbero e si l'individuo manifesterebbe una neutralità al rischio. Se, invece, fosse convessa, il soggetto sarebbe propenso al rischio.

Questo grafico è una rappresentazione visiva del comportamento umano davanti all'incertezza.

Mostra come l’utilità non cresca proporzionalmente con il reddito e perché molte persone preferiscano una certezza minore a un’incertezza più redditizia e il “costo psicologico” del rischio.

Aspetti psicologici

Nel modello classico (utilità attesa), una persona avversa al rischio preferisce un guadagno certo inferiore rispetto a una scommessa con lo stesso valore atteso.

L’avversione al rischio è un atteggiamento comune nella maggior parte delle persone. Deriva dalla paura di perdere, anche quando esiste una possibilità di guadagno.

È un comportamento radicato nella nostra psicologia evolutiva: evitare il danno era spesso più importante che ottenere un vantaggio.

Esempio. Una persona può rifiutare una promozione che comporta maggiori responsabilità e incertezza, anche se accompagnata da un aumento di stipendio.

Questo meccanismo psicologico è stato studiato in profondità da Daniel Kahneman, premio Nobel per l’economia, che ha mostrato, con la sua Prospect Theory, come la paura della perdita tenda a prevalere sul desiderio di guadagno anche in scelte economiche razionali.

Prospect Theory

Secondo Kahneman le persone non valutano gli esiti (guadagni o perdite) in termini assoluti, bensì rispetto a un punto di riferimento percepito.

Questo spiega l'avversione alla perdita (loss aversion) che molte persone manifestano. In altre parole, le perdite pesano più dei guadagni.

Ad esempio, perdere 100€ fa più male di quanto faccia piacere guadagnarne altrettanti. Questo comportamento è apparentemente irrazionale... ma è molto frequente.

Quindi, le persone non sempre sono razionali.

Inoltre, le loro preferenze non sono stabili ma dipendono dalla situazione in cui ci si trova.

Nella sua Prospect Theory, Kahneman ha dimostrato che l’avversione al rischio non è una proprietà statica o razionale, ma un comportamento influenzato da bias cognitivi, emozioni, e dall’asimmetria psicologica tra guadagni e perdite.

Nota. La Prospect Theory è oggi uno dei pilastri della economia comportamentale. Non spiega solo l’economia: spiega come decidiamo, sbagliamo e viviamo in un mondo pieno di incertezza.

Ricchezza e avversione al rischio

L’avversione al rischio diminuisce con l’aumentare della ricchezza. Il motivo è che il valore marginale della ricchezza è decrescente: ogni euro in più ha meno valore per chi è già ricco.

Inoltre, un individuo con molte risorse può assorbire meglio una perdita, perché essa ha un impatto relativo minore sulla sua condizione economica.

Esempio. Un imprenditore con 10 milioni di euro è disposto a rischiare 100.000€ in un nuovo investimento. Un individuo con solo 10.000€ probabilmente non rischierebbe nemmeno 1.000€.

La differenza tra l'avversione assoluta e relativa al rischio

Si può distinguere tra due tipi di misurazione dell'avversione al rischio.

Avversione assoluta al rischio (AAR)

Misura quanto un individuo odia il rischio in termini assoluti, indipendentemente dalla sua ricchezza. Si calcola così:

$$ A(x) = -\frac{U''(x)}{U'(x)} $$

Dove $U'(x)$ è la derivata prima dell'utilità marginale e $U''(x)$ è la derivata seconda, quella che indica la concavità della funzione.

• Se $A(x) > 0$, sei avverso al rischio.
• Se $A(x) = 0$, sei neutrale.
• Se $A(x) < 0$, sei propenso al rischio (tipo uno che compra bitcoin coi soldi del mutuo).

L'indicatore A(x) è il tasso a cui sei disposto a pagare per eliminare il rischio per ogni livello di ricchezza. Più è alto, più sei prudente.

Avversione relativa al rischio (ARR)

Misura l'avversione al rischio tenendo conto la ricchezza della persona. In altre parole, quanto ti dà fastidio rischiare in base a quanto sei ricco.

$$ R(x) = -x \cdot \frac{U''(x)}{U'(x)} = x \cdot A(x) $$

È semplicemente l’avversione assoluta $ A(x) $ moltiplicata per la ricchezza $ x $.

• Se R(x) è costante, vuol dire che se raddoppi la tua ricchezza, sei disposto a rischiare il doppio.
• Se R(x) aumenta con x, diventi più prudente man mano che diventi più ricco.
• Se R(x) diminuisce con x, diventi meno prudente man mano che diventi ricco (cioè ti puoi permettere di perdere). In genere è il caso più realistico.

E così via.