La funzione di utilità

La funzione di utilità è uno strumento matematico usato per rappresentare le preferenze di un consumatore. A ogni combinazione di beni (paniere) assegna un valore numerico che riflette il livello di soddisfazione ottenuto. \[ U = U(x_1, x_2, \dots, x_n) \] Dove \(x_1, x_2, ..., x_n\) sono le quantità consumate di ciascun bene.

Questo valore può essere usato per confrontare alternative e studiare il comportamento economico degli individui.

La funzione di utilità è una rappresentazione semplice ma potente delle preferenze individuali.

A cosa serve? Serve per confrontare panieri di beni, tracciare curve di indifferenza, modellare scelte razionali in economia e oltre. Comprenderla è essenziale per chi studia microeconomia o lavora con sistemi decisionali automatici. 

Come funziona la funzione di utilità

La funzione di utilità associa a ogni paniere di beni un numero che misura quanto è gradito al consumatore. Esistono due modi per interpretare questo numero:

• Utilità ordinale: indica solo l’ordine delle preferenze (qual è preferito, ma non di quanto).
• Utilità cardinale: indica anche l’intensità della preferenza (quanto è più gradito un paniere rispetto a un altro).

Ad esempio, se un consumatore assegna utilità 10 al paniere A e 9 al paniere B, posso dire che A è preferito a B. Se l’utilità è ordinale, so solo che A è meglio di B perché U_A>U_B ossia 10>9. Se è cardinale, so anche che A è "appena meglio" (ossia meglio ma di poco) perché U_A-U_B=10-9=1.

La forma matematica della funzione

La funzione di utilità ha la forma seguente:

\[ U = U(x_1, x_2, \dots, x_n) \]

Dove \(x_1, x_2, ..., x_n\) sono le quantità consumate di ciascun bene.

La funzione restituisce l'utilità totale ottenuta dal consumatore.

Esempio. Se un consumatore compra pane (\(x_1\)) e latte (\(x_2\)), la funzione potrebbe essere:  \[ U(x_1, x_2) = x_1^{0.5} \cdot x_2^{0.5} \]  Questa forma indica che il consumatore vuole equilibrio tra pane e latte.

Dal punto di vista grafico la funzione si presenta come una curva che cresce con la quantità consumata dei beni.

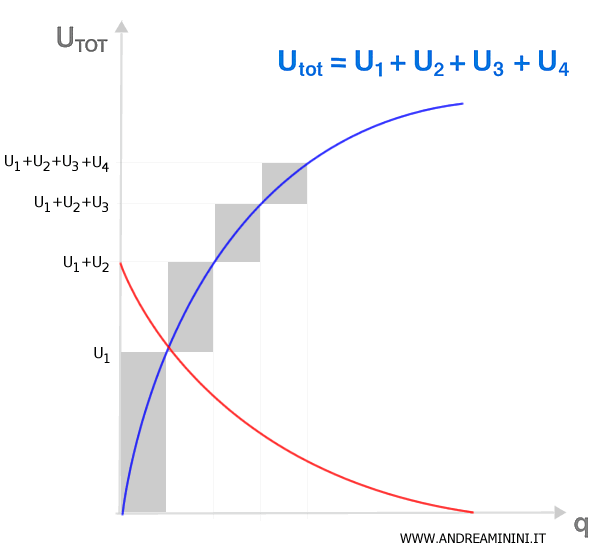
Tuttavia, la crescita dell'utilità è meno che proporzionale: tende a ridursi progressivamente a causa di un fenomeno noto come legge dell'utilità marginale decrescente.

Come si confrontano i panieri

Mettiamo che il consumatore abbia a disposizione due panieri composti con diverse quantità di beni.

Ad esempio, ecco due panieri.

• A = (2 buste di latte, 1 kg di pane, 2 kg pasta, 3 litri d'acqua)
• B = (1 busta di latte, 2 kg di pane, 1 kg pasta, 4 litri d'acqua)

I due panieri sono composti dagli stessi beni ma in quanità differenti.

La funzione permette di confrontare le utilità di due panieri:

• Se \(U(A) > U(B)\), A è preferito a B
• Se \(U(A) < U(B)\), B è preferito a A
• Se \(U(A) = U(B)\), il consumatore è indifferente tra A e B. 

Esempio. Mettiamo che la funzione di utilità sia  \[ U(x_1, x_2, x_3, x_4) = x_1^{0.5} \cdot x_2^{2} \cdot x_2^{3} \cdot x_4^{0.5} \] Dove x₁ è la quantità di latte, x₂ quella del pane, x₃ di pasta e x₄ d'acqua. Sostituendo le quantità dei beni presenti nei panieri A e B ottengo due totali. $$ U(A) = 2^{0.5}+1^2+2^3+3^{0.5} = 12.14 $$ $$ U(B) = 1^{0.5}+2^2+1^3+4^{0.5} = 8 $$ I due panieri forniscono un'utilità diversa $ U(A)=12.14 $ e $ U(B)=8 $. Quindi, il paniere A è preferito al paniere B, perché fornisce un'utilità maggiore U(A)>U(B).

Ovviamente, ogni consumatore ha le proprie preferenze proprie, quindi le sue scelte sono individuali.

Di conseguenza, non esiste una funzione di utilità valida per tutti, ciascun consumatore ha la sua.

Le curve di indifferenza

I panieri che danno la stessa utilità formano una curva di indifferenza.

Ogni punto su questa curva rappresenta una combinazione di beni che il consumatore giudica equivalente a livello di soddisfazione.

Esempio. Se un consumatore è indifferente tra il paniere A (2 mele e 3 banane) e il paniere B (3 mele e 2 banane), significa che entrambi forniscono lo stesso livello di utilità e si collocano sulla stessa curva di indifferenza.

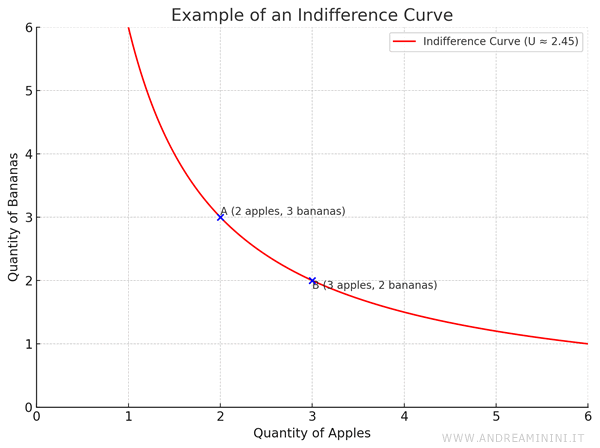
La curva comprende molte altre combinazioni che garantiscono lo stesso livello di utilità. Ad esempio, anche i panieri con 6 mele e 1 banana oppure 6 banane e 1 mela offrono la stessa soddisfazione dei panieri A e B.

Le curve di indifferenza sono uno strumento grafico per capire come il consumatore sceglie, a parità di soddisfazione, tra alternative diverse.

Note

Alcune osservazioni personali e note a margine

• Altri ambiti di applicazione
  La funzione di utilità non è usata solo in economia. È fondamentale anche in altri settori. Ad esempio, nell'intelligenza artificiale serve a modellare il comportamento degli agenti razionali: un algoritmo sceglie l’azione con la massima utilità prevista.

  Esempio pratico. Un robot domestico sceglie se pulire, ricaricarsi o riposare, assegnando una “utilità” a ogni azione in base allo stato della casa e della batteria.

 E così via.